- Research
- Open access
- Published:
An efficient algorithm to compute marginal posterior genotype probabilities for every member of a pedigree with loops
Genetics Selection Evolution volume 41, Article number: 52 (2009)
Abstract
Background
Marginal posterior genotype probabilities need to be computed for genetic analyses such as geneticcounseling in humans and selective breeding in animal and plant species.
Methods
In this paper, we describe a peeling based, deterministic, exact algorithm to compute efficiently genotype probabilities for every member of a pedigree with loops without recourse to junction-tree methods from graph theory. The efficiency in computing the likelihood by peeling comes from storing intermediate results in multidimensional tables called cutsets. Computing marginal genotype probabilities for individual i requires recomputing the likelihood for each of the possible genotypes of individual i. This can be done efficiently by storing intermediate results in two types of cutsets called anterior and posterior cutsets and reusing these intermediate results to compute the likelihood.
Examples
A small example is used to illustrate the theoretical concepts discussed in this paper, and marginal genotype probabilities are computed at a monogenic disease locus for every member in a real cattle pedigree.
Background
For monogenic or oligogenic traits, algorithms for efficient likelihood computations have been described for both pedigrees without loops [1], and pedigrees with loops [2–5] Furthermore, efficient algorithms have been developed to draw samples from the joint posterior distribution of genotypes from complex pedigrees [6, 7]. However, when pedigrees are large with many loops and multiple loci, these sampling methods can become very inefficient, and the J-PCS algorithm was proposed to address this problem [8]. This algorithm involves a) modifying the pedigree by cutting some loops and b) sampling the genotype of an individual i that is as distant as possible from the modifications ("cuts"). This sample must be drawn from the marginal posterior genotype probability distribution of i given the modified pedigree, which may still have many loops. Furthermore, marginal posterior genotype probabilities are needed in genetic counseling in humans and selective breeding in domesticated species. An efficient, exact, deterministic algorithm is available to compute the marginal posterior genotype probabilities for every member in a pedigree without loops [9]. However, it is not straightforward how to extend this algorithm to compute marginal posterior genotype probabilities for pedigrees with loops. Recently, junction tree methods from graph theory were used to describe an efficient algorithm to compute marginal posterior genotype probabilities for pedigrees with loops [10]. Most geneticists, however, are not familiar with junction tree concepts, and thus such algorithms would not readily be incorporated in genetic analyses, especially because the paper of Lauritzen and Sheehan [10] is not self-contained, but relies on results from other sources. In this paper, we present a self-contained description of an efficient, exact, deterministic algorithm to compute marginal posterior genotype probabilities for every member of a pedigree with loops, without use of junction tree methods. This algorithm has been implemented in the public domain software package MATVEC and can be obtained from the corresponding author.
Following is a brief outline of the presentation. First we define pedigree loops. Next we discuss the relationship between the likelihood and marginal posterior genotype probabilities of pedigree members. Following this, anterior and posterior cutsets are introduced. Anterior cutsets are used to compute the likelihood by the Elston-Stewart algorithm (peeling), and anterior and posterior cutsets are used to describe an efficient algorithm to calculate marginal probabilities for every member of a pedigree with loops. Next, marginal genotype probabilities are calculated for every member in a cattle pedigree that contains loops. Finally, in the appendix, a small example is used to illustrate in detail the theoretical concepts discussed in this article.
Methods
Definition of Pedigree Loops
Here we define pedigree loops indirectly by providing a simple algorithm to determine if a pedigree contains loops. A pedigree is a set of individuals, each of which can be classified as a founder or a non-founder. A founder is a pedigree member whose parents are not in the pedigree, and a non-founder is a pedigree member with both parents present in the pedigree. A nuclear family consists of a set of parents and all their off spring. A terminal family is a family that has at most one member who belongs to at least one other nuclear family. Terminal members of a pedigree are members of terminal families that do not belong to another family. The algorithm used to determine if a pedigree contains loops relies on identifying and then eliminating terminal members from the pedigree. If a pedigree does not contain any loops, repeated removal of terminal members from the pedigree will result in all members being removed from the pedigree. On the other hand, if a pedigree contains any loops, not all members of the pedigree can be removed by repeated removal of terminal members. See additional file 1: "Algorithm to detect loops.pdf" for an example of the use of this algorithm to identify loops in arbitrary pedigrees.
Likelihood and Genotype Probability Calculations for General Pedigrees
Consider a pedigree with n individuals, and let g i denote the possible genotype and y i the observed phenotype of an arbitrary pedigree member i. Note that both g i and y i can be a function of a single locus or of multiple loci on the chromosome. The likelihood for a genetic model given the observed data can be written as

where F(g, y; ρ, q, θ) denotes the joint distribution of all g i (g) and all y i (y) in the pedigree, ρ is the vector of recombination rates between loci, q is the vector of gene frequencies, and θ is the vector of parameters in the genetic model that relates y i and g i [11]. Furthermore, the likelihood can be written as

where  is a set of possible genotypes of a given set of pedigree members s
i
, and
is a set of possible genotypes of a given set of pedigree members s
i
, and  is defined as
is defined as

where h(y
i
| g
i
, θ) is the conditional probability of the phenotype y
i
given the genotype g
i
(also known as the penetrance function of individual i), Pr(g
i
| q) is the marginal probability that a founder has genotype g
i
(founder probability) and Pr(g
i
|  ,
,  , ρ) is the probability that a non-founder has genotype g
i
given that its mother (m
i
) has genotype
, ρ) is the probability that a non-founder has genotype g
i
given that its mother (m
i
) has genotype  and its father (f
i
) has genotype
and its father (f
i
) has genotype  (transition probability). When g
i
,
(transition probability). When g
i
,  and
and  consist of multiple loci, the multilocus transition probability can be written as a product of single-locus transition probabilities and recombination probabilities between adjacent loci, by making use of the Markov property for recombination events between adjacent loci that holds under the assumption of no interference [5, 12]. Note that, for each individual i in the pedigree, a set s
i
is defined that contains either one or three individuals. For founders, s
i
contains only i, while for non-founders, s
i
contains i, m
i
and f
i
. For an arbitrary pedigree member i, marginal genotype probabilities can be written as
consist of multiple loci, the multilocus transition probability can be written as a product of single-locus transition probabilities and recombination probabilities between adjacent loci, by making use of the Markov property for recombination events between adjacent loci that holds under the assumption of no interference [5, 12]. Note that, for each individual i in the pedigree, a set s
i
is defined that contains either one or three individuals. For founders, s
i
contains only i, while for non-founders, s
i
contains i, m
i
and f
i
. For an arbitrary pedigree member i, marginal genotype probabilities can be written as

where L is the likelihood defined in 2, and  is the likelihood computed with g
i
fixed at genotype x. Thus, the efficient computation of marginal genotype probabilities using equation 4 requires an efficient algorithm to compute the likelihood. The computation of the likelihood using 2 is not efficient for pedigrees having more than about 20 members. However, the Elston-Stewart algorithm, which is also known as peeling, can be used to efficiently compute the likelihood [1, 13]. Still, using equation 4 to compute marginal probabilities for N unknown genotypes of individual i requires recomputing the likelihood with g
i
= x for each of the N values of x. Furthermore, this has to be repeated for all n individuals in the pedigree. In the following section we introduce an algorithm to avoid repeating computations by storing intermediate results in multidimensional tables called anterior and posterior cutsets.
is the likelihood computed with g
i
fixed at genotype x. Thus, the efficient computation of marginal genotype probabilities using equation 4 requires an efficient algorithm to compute the likelihood. The computation of the likelihood using 2 is not efficient for pedigrees having more than about 20 members. However, the Elston-Stewart algorithm, which is also known as peeling, can be used to efficiently compute the likelihood [1, 13]. Still, using equation 4 to compute marginal probabilities for N unknown genotypes of individual i requires recomputing the likelihood with g
i
= x for each of the N values of x. Furthermore, this has to be repeated for all n individuals in the pedigree. In the following section we introduce an algorithm to avoid repeating computations by storing intermediate results in multidimensional tables called anterior and posterior cutsets.
Anterior and Posterior Cutsets
Computing the likelihood by peeling involves summing over the genotypes of one individual at a time and storing the intermediate results. For convenience, here we assume that individuals are numbered in the order that they are peeled. Peeling the first individual amounts to computing the sum over g1 of the product of all factors in 2 that contain g1, for each combination of the other genotypes that occur together with g1. Results of these summations are stored in a multidimensional table that has been called a cutset [13]. Here we will refer to these tables as anterior cutsets. The anterior cutset obtained after peeling g1 will be denoted by  and is calculated as
and is calculated as

where V1 is a set of pedigree members defined as follows. Using the sets s
i
defined earlier for each individual in the pedigree, U1 is defined as the union of all s
j
that contain individual 1. Then V1 is obtained by removing individual 1 from U1. Further,  is the set of genotypes for the individuals in V1. Note that the product in 5 is over those pedigree members j that contain individual 1 in their s
j
.
is the set of genotypes for the individuals in V1. Note that the product in 5 is over those pedigree members j that contain individual 1 in their s
j
.
Replacing in 2 the product of all factors containing g1, summed over g1, with  gives the following expression for the likelihood
gives the following expression for the likelihood

where g1 = {g2 ... g n } is the set of possible genotypes of the individuals that remain to be peeled, and the product is over those pedigree members r that do not contain individual 1 in their s r . The likelihood expressed as above after peeling g1, will be referred to as LE1, and in general after peeling g i , will be referred as LE i .
Note that after g1 has been peeled, the summation in 6 is only over the genotypes of individuals 2 ... n. As described below, and later illustrated through a hypothetical example in the Appendix, as each individual is peeled, an anterior cutset is generated. After peeling the last individual, the final anterior cutset will have only a single value that is equal to the likelihood. Note that for a pedigree with n members, there are n! possible peeling orders. Although any choice of a peeling sequence will lead to the same value for the likelihood, not all choices of the peeling sequence lead to anterior cutsets of the same size. As the amount of memory required does depend on the size of the cutsets, a peeling sequence leading to smaller cutsets is more desirable. However, even for moderately large n, an exhaustive search for an efficient peeling sequence is not feasible. Furthermore, there is no known algorithm to efficiently find the peeling order with the lowest storage requirements [10]. However, the following simple heuristic procedure can be used to generate a good peeling sequence. At any stage of the peeling process, in order to decide which individual should be peeled next, for each individual i that remains to be peeled, we compute the size of the anterior cutset that would be generated by peeling i. The individual with the smallest anterior cutset size is chosen to be peeled next [14].
Now it is convenient to introduce the posterior cutset which will be used to avoid repeating computations in calculating genotype probabilities. By factoring out  from 6 and by summing over the genotypes of all remaining pedigree members not contained in V1, we can define a second multidimensional table called a posterior cutset
from 6 and by summing over the genotypes of all remaining pedigree members not contained in V1, we can define a second multidimensional table called a posterior cutset

where  is not a function of g1. As a result we can rewrite the likelihood as follows
is not a function of g1. As a result we can rewrite the likelihood as follows

In the general description of peeling given below, we make extensive use of two sets defined for each individual i. The first set s i has already been described earlier, and it is completely determined by the pedigree. The second set V i contains the individuals in the cutset that is generated when i is peeled. Thus, V i is determined by the pedigree and the peeling order. In general, peeling individual i amounts to computing the sum over g i of the product of all factors in LEi-1that contain g i , for each combination of the other genotypes that occur together with g i . These summations are stored in the anterior cutset for i:

where j is an individual whose function f
j
( ) remains in LEi-1and i ∈ s
j
, k is an individual whose anterior cutset
) remains in LEi-1and i ∈ s
j
, k is an individual whose anterior cutset  remains in LEi-1and i ∈ V
k
, U
i
= (
remains in LEi-1and i ∈ V
k
, U
i
= ( ) ∪ (∪ V
k
), and V
i
= U
i
-i. Replacing in LEi-1the sum over g
i
of the product of all factors containing g
i
with
) ∪ (∪ V
k
), and V
i
= U
i
-i. Replacing in LEi-1the sum over g
i
of the product of all factors containing g
i
with  gives the likelihood expression LE
i
:
gives the likelihood expression LE
i
:

where  are the functions from LEi-1that were not used in the calculation of
are the functions from LEi-1that were not used in the calculation of  and
and  are the anterior cutsets from LEi-1that were not used in the calculation of
are the anterior cutsets from LEi-1that were not used in the calculation of  . Now we obtain the posterior cutset for i by removing
. Now we obtain the posterior cutset for i by removing  from LE
i
:
from LE
i
:

Note that  is not a function of g
i
. Thus, in general we can write the likelihood as follows
is not a function of g
i
. Thus, in general we can write the likelihood as follows

Now we are ready to explain how to compute genotype probabilities for any individual m ∈ V i using anterior and posterior cutsets. As in equation 4, marginal genotype probabilities for m can be written as

The denominator of 13 is given by 12, while the numerator is obtained by computing 12 with g
m
fixed at x. If m is in more than one set of pedigree members V
i
, identifying the set V
i
with smallest number of members will minimize the required computations. However, if m is not in any V
i
, we first write the likelihood 12 as a product of the anterior and posterior cutsets for m. In this expression, however, m has already been peeled. Equation 9, which is used to compute the anterior cutset for an arbitrary individual, contains that individual prior to it being peeled. Thus, by substituting in 12, the expression given in 9 for  gives
gives

Now the numerator of 13 is obtained by computing 14 with g m fixed at x.
Provided a good peeling sequence is available, computation of the required anterior cutsets and the summation over 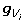 in 12 or
in 12 or  in 14 would be feasible. However, posterior cutsets cannot be computed efficiently using 11 because here the summation may be over a very large set of genotypes. Fortunately, posterior cutsets can be computed recursively as described below. Although the derivation of the recursive algorithm given below is conceptually straightforward, it may be tedious to follow. Thus, at the end of this section, we provide four easy to implement steps to efficiently compute posterior cutsets.
in 14 would be feasible. However, posterior cutsets cannot be computed efficiently using 11 because here the summation may be over a very large set of genotypes. Fortunately, posterior cutsets can be computed recursively as described below. Although the derivation of the recursive algorithm given below is conceptually straightforward, it may be tedious to follow. Thus, at the end of this section, we provide four easy to implement steps to efficiently compute posterior cutsets.
The key principle that we have used to compute marginal posterior probabilities efficiently is that any pedigree member can be assigned into one of three mutually exclusive sets with respect to any individual i: the set of members that contribute to  , the set of members that contribute to
, the set of members that contribute to  , or the set of members in V
i
. For example, in computing the numerator of 13 by using 12, the intermediate results from peeling individuals in the first set were stored in
, or the set of members in V
i
. For example, in computing the numerator of 13 by using 12, the intermediate results from peeling individuals in the first set were stored in  and used repeatedly, the intermediate results from peeling individuals in the second set were stored in
and used repeatedly, the intermediate results from peeling individuals in the second set were stored in  and used repeatedly, and only the calculations for peeling individuals in the third set were repeated. This principle of factoring the likelihood into anterior and posterior components is used repeatedly in the following derivations. To derive the recursive algorithm, first we establish that
and used repeatedly, and only the calculations for peeling individuals in the third set were repeated. This principle of factoring the likelihood into anterior and posterior components is used repeatedly in the following derivations. To derive the recursive algorithm, first we establish that  = 1.0, which is the base case of the recursion. Similar to 10, after peeling individual n - 1, the likelihood expression LEn-1becomes
= 1.0, which is the base case of the recursion. Similar to 10, after peeling individual n - 1, the likelihood expression LEn-1becomes

Because only individual n remains to be peeled, V u and Vn-1contain only n. The likelihood now becomes

Further, using 9,  can be written as
can be written as

Note that in 16 and 17 the right-hand sides are identical, and thus L =  . However, from 12
. However, from 12

and thus  = 1.0. Now, for any other individual i,
= 1.0. Now, for any other individual i,  can be computed recursively as follows.
can be computed recursively as follows.
The anterior cutset  generated when i is peeled, is used in the calculation of the anterior cutset generated when k = min(V
i
) is peeled. The resulting anterior cutset can be written as
generated when i is peeled, is used in the calculation of the anterior cutset generated when k = min(V
i
) is peeled. The resulting anterior cutset can be written as

where  are all remaining functions with k ∈ s
r
, and
are all remaining functions with k ∈ s
r
, and  are the remaining anterior cutsets with k ∈ V
j
in addition to
are the remaining anterior cutsets with k ∈ V
j
in addition to  . Similar to (12) we can also write
. Similar to (12) we can also write

and by using (19) in (20) we can write

Recall that we have defined the set of individuals U k = V k ∪ {k}, and thus we can write

Note that both (12) and (22) contain the term  . By rearranging 22, the likelihood can be written as
. By rearranging 22, the likelihood can be written as

and using 12 we can write

Thus, the posterior cutset for individual i can be expressed as a function of some anterior cutsets and the posterior cutset for individual k > i. Starting at individual n - 1 all posterior cutsets can be computed in the reverse order of peeling because  = 1.0.
= 1.0.
In summary, the following procedure can be used to recursively compute the posterior cutset of an arbitrary individual i in a pedigree:
-
1.
Compute anterior cutsets for all individuals in the pedigree. This step is done only once.
-
2.
Identify the anterior cutset
 whose summand contains the factor
whose summand contains the factor  (see equation 19).
(see equation 19). -
3.
Replace
 in the summand of
in the summand of  with
with 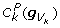 , and for each value of
, and for each value of 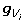 sum over the remaining genotypes in this expression (see equation 24).
sum over the remaining genotypes in this expression (see equation 24). -
4.
If
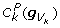 has not been computed yet, use steps 2, 3 and 4 to compute it (this is the recursion).
has not been computed yet, use steps 2, 3 and 4 to compute it (this is the recursion).
Note that to compute marginal posterior genotype probabilities for an arbitrary member of the pedigree using this algorithm, we need to calculate all anterior cutsets and a subset of all posterior cutsets. Both the anterior and the posterior cutset of a given individual have the same size. The computation of an anterior cutset involves the summation over the genotypes of one individual. The computation of a posterior cutset can involve summations over the genotypes of a variable number individuals. The theoretical concepts introduced in this section are illustrated in detail for a simple example in the Appendix. In the following section we discuss a real data application of the theoretical concepts described above.
Genotype Probabilities Computations in a Real Cattle Pedigree
Consider the pedigree given in the first three columns of Table 1 with a graphical representation given in Figure 1. Six terminal members of this cattle pedigree (individuals A21, A22, A23, A24, A25 and A26) are known to be affected by a monogenic recessive disease. Conditional on disease status, assumed mode of inheritance, pedigree information, and on the assumption that the frequency of the recessive allele in the cattle population from which the pedigree was sampled is equal to 0.00001, we calculate genotype probabilities for every member of the pedigree using the algorithm described above. Of the six founders present in this cattle pedigree, founder individual A2 is identified to be a carrier of the recessive allele with probability 1.0. Selective breeding decisions can be made given the calculated posterior genotype probabilities.
Next, we augment the genetic information used to calculate posterior genotype probabilities, by including genetic data on two marker loci flanking the hypothesized position of the recessive locus. Each marker locus has three alleles and the two loci are separated by 0.8 cM with the hypothesized position of the recessive locus 0.5 cM from the left marker (M1). The allele scores of the two markers used are given in Table 2. The impact of the additional information provided by the marker data is reflected in the posterior probability of individuals A19 and A20 being carriers of the recessive allele (Table 3). While without marker data individuals A19 and A20 have a posterior probability of being carriers equal to 0.6667, with marker data the probability is close to one.
Discussion
As stated by Jensen and Kong [15] current algorithms for calculating marginal posterior genotype probabilities by peeling are inefficient. As described earlier, computing marginal genotype probabilities for individual j using equation 13, requires recomputing the likelihood for each of the possible genotypes of individual j. For the last individual in the peeling sequence, this can be done efficiently because intermediate results from peeling individuals 1 through n - 1, for each possible value of g
n
, have been stored in the anterior cutset  . Thus, by making use of the intermediate results stored in
. Thus, by making use of the intermediate results stored in  , only calculations from the last step of peeling need to be repeated to compute
, only calculations from the last step of peeling need to be repeated to compute  . For any m that is in more than one set V
i
we identify the smallest V
i
containing m. The intermediate results from peeling individuals 1 through i are stored in anterior cutsets, including
. For any m that is in more than one set V
i
we identify the smallest V
i
containing m. The intermediate results from peeling individuals 1 through i are stored in anterior cutsets, including  , and do not have to be recomputed. In this paper we have introduced a second type of cutset, called a posterior cutset, together with an algorithm for its efficient computation. The posterior cutset
, and do not have to be recomputed. In this paper we have introduced a second type of cutset, called a posterior cutset, together with an algorithm for its efficient computation. The posterior cutset  contains the intermediate results from peeling all individuals that did not contribute to
contains the intermediate results from peeling all individuals that did not contribute to  and are not contained in the set V
i
. Thus, by making use of the intermediate results stored in both
and are not contained in the set V
i
. Thus, by making use of the intermediate results stored in both  and
and  , only calculations associated with peeling individuals in V
i
(except m) need to be repeated to compute the numerator
, only calculations associated with peeling individuals in V
i
(except m) need to be repeated to compute the numerator  of 13. For any m that is not in any V
i
the expression used to compute genotype probabilities (14) cannot be written as a product of a single anterior and posterior. However, any of the anterior the posterior cutsets used in 14 can be computed efficiently. Thus, this new peeling based algorithm provides an efficient method to compute marginal genotype probabilities for an arbitrary member of a pedigree with loops. The computational cost of obtaining posterior genotype probabilities for all members of a pedigree would approximately be equal to twice that of computing the likelihood because computing the likelihood only requires computing the anterior cutsets while computing all genotype probabilities would require computing the posterior cutsets also. As stated by Jensen and Kong [15], a peeling based algorithm would be more accessible to researchers in genetics than the currently available junction-tree methods [10].
of 13. For any m that is not in any V
i
the expression used to compute genotype probabilities (14) cannot be written as a product of a single anterior and posterior. However, any of the anterior the posterior cutsets used in 14 can be computed efficiently. Thus, this new peeling based algorithm provides an efficient method to compute marginal genotype probabilities for an arbitrary member of a pedigree with loops. The computational cost of obtaining posterior genotype probabilities for all members of a pedigree would approximately be equal to twice that of computing the likelihood because computing the likelihood only requires computing the anterior cutsets while computing all genotype probabilities would require computing the posterior cutsets also. As stated by Jensen and Kong [15], a peeling based algorithm would be more accessible to researchers in genetics than the currently available junction-tree methods [10].
Throughout this paper the likelihood was written as a sum over genotype variables. However, when the genotype of an individual is defined over k loci, the number of genotypes increases exponentially with k. In such situations, writing the likelihood as a sum over allele state and origin allele variables may lead to more efficient computations [12]. Algorithms presented in this paper can be used to calculate the posterior allele state and allele origin probabilities by peeling over allele state and allele origin variables.
Appendix
The pedigree given in Figure 2 will be used to illustrate the theoretical concepts discussed above.
First we show how to use the Elston-Stewart algorithm to compute the likelihood for a genetic model given this pedigree. Next we describe how to calculate marginal posterior genotype probabilities for an arbitrary member of this pedigree using the efficient algorithm described above.
Likelihood computations by peeling
As shown in 2, the likelihood given the observed data can be written as

In the pedigree given in Figure 2, individuals are numbered according to a suitable peeling sequence. Note that in 25 f1(g5, g4, g1) is the only function that involves g1. Peeling g1 amounts to computing the sum over g1 of f1(g5, g4, g1), for each combination of the genotypes for individuals 5 and 4, and storing the results of these summations in the anterior cutset

Note that  is a two dimensional table of size N5 × N4, where N5 and N4 are the number of possible genotypes for individuals 5 and 4. Replacing the sum over g1 of f1(g5, g4, g1) in 25 with
is a two dimensional table of size N5 × N4, where N5 and N4 are the number of possible genotypes for individuals 5 and 4. Replacing the sum over g1 of f1(g5, g4, g1) in 25 with  gives the likelihood expression LE1:
gives the likelihood expression LE1:

Note that in LE1f2(g5, g4, g2) is the only function that involves g2. Therefore, the anterior cutset for 2 (obtained by peeling g2) is

Replacing the sum over g2 of f2(g5, g4, g2) in LE1 with  gives the likelihood expression LE2:
gives the likelihood expression LE2:

Note that in LE2f3(g5, g4, g3) is the only function that involves g3. Therefore, the anterior cutset for 3 (obtained by peeling g3) is

Replacing the sum over g3 of f3(g5, g4, g3) in LE2 with  gives the likelihood expression LE3:
gives the likelihood expression LE3:

Note that in LE3 not only f4(g7, g6, g4), but also  ,
,  and
and  involve g4. Thus, peeling g4 yields the following anterior cutset
involve g4. Thus, peeling g4 yields the following anterior cutset

The resulting anterior cutset  is a three dimensional table of size N7 × N6 × N5, where N7, N6 and N5 are the number of possible genotypes for individuals 7, 6 and 5.
is a three dimensional table of size N7 × N6 × N5, where N7, N6 and N5 are the number of possible genotypes for individuals 7, 6 and 5.  replaces in LE3 the factors f4(g7, g6, g4),
replaces in LE3 the factors f4(g7, g6, g4),  ,
,  and
and  summed over g4. Thus, the likelihood expression LE4 becomes
summed over g4. Thus, the likelihood expression LE4 becomes

Note that in LE4 both f5(g7, g6, g5) and  involve g5. Peeling g5 yields the following anterior cutset
involve g5. Peeling g5 yields the following anterior cutset

This cutset replaces in LE4 the factors f5(g7, g6, g5) and  summed over g5. Thus, the likelihood expression LE5 becomes
summed over g5. Thus, the likelihood expression LE5 becomes

In LE5 both f6(g6) and  involve g6. Peeling g6 yields the following anterior cutset
involve g6. Peeling g6 yields the following anterior cutset

By replacing f6(g6) and  summed over g6 with
summed over g6 with  in LE5, the likelihood expression LE6 becomes
in LE5, the likelihood expression LE6 becomes

Note, however, that the anterior cutset obtained by peeling g7 yields the numerical value

and thus the likelihood expression LE7:

Genotype probability computations
Recall that for an arbitrary member of the pedigree (e.g. individual 3) we can calculate marginal genotype probabilities as follows

where  is the likelihood computed with g3 fixed at x. As discussed earlier, using this procedure to compute marginal genotype probabilities for N unknown genotypes of individual 3 requires recomputing the likelihood for the entire pedigree N times. However by writing the likelihood as in 12, these computations can be done efficiently. Consider computing marginal posterior genotype probabilities for individual 3. Recall that, as shown in 26,
is the likelihood computed with g3 fixed at x. As discussed earlier, using this procedure to compute marginal genotype probabilities for N unknown genotypes of individual 3 requires recomputing the likelihood for the entire pedigree N times. However by writing the likelihood as in 12, these computations can be done efficiently. Consider computing marginal posterior genotype probabilities for individual 3. Recall that, as shown in 26,  = Σg 3f3(g5, g4, g3). Using this in 12 we obtain
= Σg 3f3(g5, g4, g3). Using this in 12 we obtain

Note that 32 can be used to calculate the denominator of 31, while the numerator of 31 can be obtained by fixing g3 in 32 at x. To complete the calculations, however, we need to compute  . This is done using the recursive procedure described previously as shown below.
. This is done using the recursive procedure described previously as shown below.
Step 1 of the procedure is to compute anterior cutsets for all individuals in the pedigree, and this has already been done. Following step 2, we determine that  contributes to the computation of
contributes to the computation of  (see equation 27). Following step 3,
(see equation 27). Following step 3,  is replaced with
is replaced with  in 27 and, for each value of g4 and g5, the sum over g7 and g6 is computed to obtain
in 27 and, for each value of g4 and g5, the sum over g7 and g6 is computed to obtain

Following step 4, note that  is not computed yet. Thus, steps 2, 3 and 4 are repeated as follows.
is not computed yet. Thus, steps 2, 3 and 4 are repeated as follows.
Following step 2, we determine that  contributes to the computation of
contributes to the computation of  (see equation 28). Following step 3,
(see equation 28). Following step 3,  is replaced with
is replaced with  in 28 and, for each value of g7, g6 and g5, we obtain
in 28 and, for each value of g7, g6 and g5, we obtain

Following step 4, note that  is not computed yet. Thus, steps 2, 3 and 4 are repeated as follows.
is not computed yet. Thus, steps 2, 3 and 4 are repeated as follows.
Following step 2, we determine that  contributes to the computation of
contributes to the computation of  (see equation 29).
(see equation 29).
Following step 3,  is replaced with
is replaced with  in 29 and, for each value of g7 and g6 we obtain
in 29 and, for each value of g7 and g6 we obtain

Following step 4, note that  is not computed yet. Thus, steps 2, 3 and 4 are repeated as follows.
is not computed yet. Thus, steps 2, 3 and 4 are repeated as follows.
Following step 2, we determine that  contributes to the computation of
contributes to the computation of  (see equation 30).
(see equation 30).
Following step 3,  is replaced with
is replaced with  in 30 and, for each value of g7 we obtain
in 30 and, for each value of g7 we obtain

Following step 4, note that  = 1.0, and thus the calculations for
= 1.0, and thus the calculations for  can be completed. Now using
can be completed. Now using  , the calculations for
, the calculations for  can be completed, and using
can be completed, and using  , the calculations for
, the calculations for  can be completed. Finally, using
can be completed. Finally, using  , the calculations for
, the calculations for  can be completed.
can be completed.
References
Elston RC, Stewart J: A general model for the genetic analysis of pedigree data. Human Hered. 1971, 21: 523-542. 10.1159/000152448.
Lange K, Elston RC: Extension to pedigree analysis. I. Likelihood calculations for simple and complex pedigrees. Hum Hered. 1975, 25: 95-105. 10.1159/000152714.
Cannings C, Thompson EA, Skolnick MH: Probability functions on complex pedigrees. Adv Appl Prob. 1978, 10: 26-61. 10.2307/1426718.
Thomas A: Approximate computation of probability functions for pedigree analysis. IMA J Math Appl Med Biol. 1986, 3: 157-166. 10.1093/imammb/3.3.157.
Lander ES, Green P: Construction of multilocus genetic linkage maps in humans. Proc Natl Acad Sci USA. 1987, 84 (8): 2363-2367. 10.1073/pnas.84.8.2363.
Heath S: Markov chain Monte Carlo segregation and linkage analysis for oligonec models. Am J Hum Genet. 1997, 61: 748-760. 10.1086/515506.
Fernández SA, Fernando RL, Gulbrandtsen B, Totir LR, Carriquiry AL: Sampling genotypes in large pedigrees with loops. Genet Sel Evol. 2001, 33: 337-367. 10.1186/1297-9686-33-4-337.
Fernando R, Totir L, Pita F, Stricker C, Abraham K: Algorithms to compute allele state and origin probabilities for QTL mapping. 8th World Congress Genet Appl Livest Prod. 2006
Fernando RL, Stricker C, Elston RC: An efficient algorithm to compute the posterior genotypic distribution for every member of a pedigree without loops. Theor Appl Genet. 1993, 87: 89-93. 10.1007/BF00223750.
Lauritzen SL, Sheehan NA: Graphical models for genetic analysis. Statist Sci. 2003, 18: 489-514. 10.1214/ss/1081443232.
Thompson E: Pedigree Analysis in Human Genetics. 1986, The Johns Hopkins University Press, Baltimore
Fishelson M, Geiger D: Exact genetic linkage computations for general pedigrees. Bioinformatics. 2002, 18: S189-S198.
Cannings C, Thompson EA, Skolnick MH: The recursive derivation of likelihoods on complex pedigrees. Adv Appl Prob. 1976, 8: 622-625. 10.2307/1425918.
Lange K, Boehnke M: Extensions to pedigree analysis. V. Optimal calculation of mendelian likelihoods. Hum Hered. 1983, 33: 291-301. 10.1159/000153393.
Jensen CS, Kong A: Blocking Gibbs sampling for linkage analysis in large pedigrees with many loops. Am J Hum Genet. 1999, 65: 885-901. 10.1086/302524.
Acknowledgements
The authors would like to thank James Reecy and James Koltes for providing the marker and phenotypic data for the real cattle pedigree discussed in this article. RLF is supported by the United States Department of Agriculture, National Research Initiative grant USDA-NRI-2007-35205-17862.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors' contributions
LRT and RLF developed and programmed the algorithm in C++. The analysis of the real cattle pedigree was performed by LRT. KJA contributed to the C++ implementation of the algorithm. The manuscript was prepared by LRT and RLF. All authors have read and approved the final manuscript.
Electronic supplementary material
12711_2009_2427_MOESM1_ESM.PDF
Additional file 1:A numerical example to illustrate algorithm to detect loops in a pedigree. Algorithm to detect loops in a pedigree. (PDF 54 KB)
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is published under license to BioMed Central Ltd. This is an Open Access article is distributed under the terms of the Creative Commons Attribution License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Totir, L.R., Fernando, R.L. & Abraham, J. An efficient algorithm to compute marginal posterior genotype probabilities for every member of a pedigree with loops. Genet Sel Evol 41, 52 (2009). https://doi.org/10.1186/1297-9686-41-52
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1297-9686-41-52

 whose summand contains the factor
whose summand contains the factor 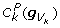 , and for each value of
, and for each value of 
